Answer:
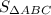 = 4·
= 4·
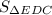
Explanation:
From the midpoint theorem, which states that the line that a line drawn such that it joins the midpoints of two sides of a triangle, is parallel to the third side of the triangle and is equal to half the length of the third side
Therefore, the lengths of the sides of ΔDEF, drawn by joining the midpoints of ΔABC is equal to half the length of and parallel to the corresponding side of ΔABC
We therefore, have that the corresponding sides of ΔABC and ΔDEF have a common ratio and a pair of sides in each triangle form same angles, therefore;
ΔDEF is similar to ΔABC by Side, Side, Side SSS similarity.
The length of the perimeter of ΔABC,
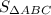 = 2 × The length of the perimeter of triangle ΔEDC,
= 2 × The length of the perimeter of triangle ΔEDC,
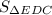
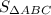 = 2 ×
= 2 ×
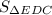
∴
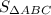 ≠ 4 ×
≠ 4 ×
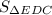
The statement which is incorrect is therefore;
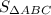 = 4 ×
= 4 ×
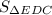 .
.