Answer:

Step-by-step explanation:
We are asked to find the time it tasked for a ball to hit the ground. We know the height, acceleration, and initial velocity, so we will use the following kinematic equation:
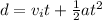
The ball starts at rest, so its initial velocity is 0 meters per second. The distance is 700 meters. The ball is in free fall, so the acceleration is due to gravity, or 9.8 meters per second squared.
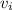 = 0 m/s
= 0 m/s - d= 700 m
- a= 9.8 m/s²
Substitute the values into the formula.
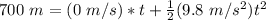
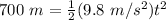
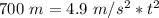
Divide both sides by 4.9 meters per second squared to isolate the variable t.
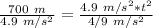
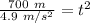
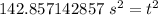
Take the square root of both sides.
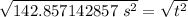
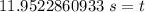
The original measurement has 3 significant figures, so our answer must have the same.
3 sig fig for our answer is the tenths place. The 5 in the tenths place tells us to round the 9 to a 0, then round the 1 to a 2.
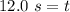
It takes the ball approximately 12.0 seconds to hit the ground.