Answer:
x approaches negative 3 to the right:
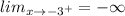
x approaches negative 3 to the left:
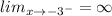
Explanation:
The function we have is:
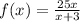
We have an asymptote at x = -3.
The limit of the function when x approaches negative 3 to the right will be:
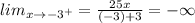
It is because the function is decreasing from right to left.
And the limit of the function when x approaches negative 3 to the left will be:
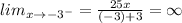
It is because the function is decreasing from left to right.
I hope it helps you!