Question

Function f (x) = 25x/x + 3 has a discontinuity at x = –3. What are Limit of f (x) as x approaches negative 3 minus and Limit of f (x) as x approaches negative 3 plus?

Answer 1

Answer: C

Explanation:

Edge

Answer 2

x approaches negative 3 to the right:
`lim_(x\to -3^(+))=-\infty`

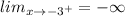
x approaches negative 3 to the left:
`lim_(x\to -3^(-))=\infty`

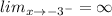
Explanation:

The function we have is:

`f(x)=(25x)/(x+3)`

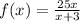
We have an asymptote at x = -3.

The limit of the function when x approaches negative 3 to the right will be:

`lim_(x\to -3^(+))=(25x)/((-3)+3)=-\infty`

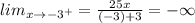
It is because the function is decreasing from right to left.

And the limit of the function when x approaches negative 3 to the left will be:

`lim_(x\to -3^(-))=(25x)/((-3)+3)=\infty`

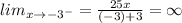
It is because the function is decreasing from left to right.

I hope it helps you!