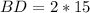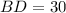Answer:
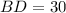
Explanation:
Given
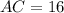
See attachment
Required
Find BD
If AC = 16, then:
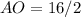 i.e. half the diagonal AC
i.e. half the diagonal AC
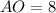
The diagonals of a rhombus are perpendicular.
This implies that we can apply Pythagoras theorem.
Using Pythagoras theorem on triangle AOB, we have:
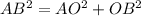
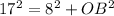
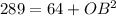
Collect like terms
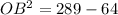
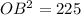
Take positive square roots of both sides
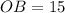
To solve for BD, we use:
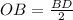 --- i.e. half the diagonal BD
--- i.e. half the diagonal BD