Question

The report "The New Food Fights: U.S. Public Divides Over Food Science" states that younger adults are more likely to see foods with genetically modified ingredients as being bad for their health than older adults. This statement is based on a representative sample of 178 adult Americans aged 18 to 29 and a representative sample of 427 adult Americans aged 50 to 64. Of those in the 18 to 29 age group, 48% said they believed these foods were bad for their health, while only 3% of those in the 50 to 64 age group believed this.

(a) Are the sample sizes large enough to use the large-sample confidence interval to estimate the difference in the population proportions? Yes Y Let - 0.48 and p =0.38, -178 and 1 = 427, where the 1 subscript indicates the age 18-29 group and the 2 subscript indicates the age 50-64 group. Since 654 n (1-P) = 92.56 - 162.26 and 2(1-2) 264.74 are all at least 10, the sample sizes are large enough to use the large-sample confidence interval
(b) Estimate the difference in the proportion of adult Americans aged 18 to 29 who believe the foods made with genetically modified ingredients are bad for their health and the corresponding proportion for adult Americans aged 50 to 64. Use a 90% confidence interval. (Use Pi - P2. Use a table or technology. Round your answers to four decimal places.) (0.02545 x 0.17083 x )
(c) Is zero in the confidence interval? Yes No What does this suggest about the difference in the two population proportions?

Answer 1

`$n_1=178, \hat p_1 = 0.48$`

`$n_2=427, \hat p_2 = 0.38$`

`$\hat p_1=(x_1)/(n_1)$`

`$x_1=n_1 \hat p_1$`

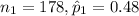
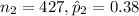
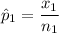
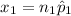
= 178 x 0.48

= 85.44

≈ 85

`$x_2=n_2 \hat p_2$`

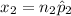
= 427 x 0.38

= 162.26

≈ 162

a). Yes, the sample sizes are large enough to use the large sample confidence interval so as to estimate the difference in the population proportions.

Let
`$\hat p_1 = 0.48, \ \ \hat p_2 = 0.38, n_1 = 178 \ \ n_2 = 427$`

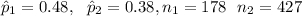
Where the
`$\text{subscript indicates}$` the age
`$18-29$` group and the 2 - subscript indicates the age
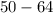`$50-64$` group.

Since
`$n_1 \hat p_1 = 85.44$`

`$n_1(1- \hat p_1)=92.56, \ \ n_2\hat p_2 = 162.26, \ n_2(1-\hat p_2) = 264.74 $`

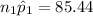
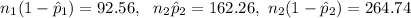
are all at least 10, the sample sizes are large enough to use the large sample confidence interval.

`$P_0=(x_1+x_2)/(n_1+n_2)$`

`$=(85.44+162.26)/(178+427)$`

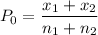
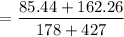
= 0.409421

`$P_0 = 0.4074$`

`$Q_0=1-P_0$`

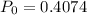
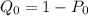
= 1 - 0.4094

= 0.5906

b). 90% confidence interval is

`$=\left( \hat p_1- \hat p_2 \pm (z \alpha)/(2) * \sqrt{P_0Q_0\left((1)/(n_1)+(1)/(n_2)}\right) \right)$`

`$=\left( 0.48-0.38 \pm (z * 0.10)/(2) * \sqrt{0.4094 * 0.5906\left((1)/(178)+(1)/(427)}\right) \right)$`

`$=(0.1 \pm z 0.05 * 0.04387082)$`

`$=(0.1 \pm 1.64 * 0.0439)$`

`$=(0.1 - 0.071996, 0.1+0.071996)$`

`$=(0.028004, 0.171996)$`

`$=(0.0280, 0.1720)$`

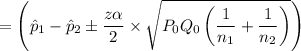
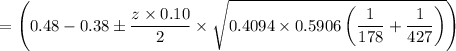
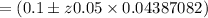
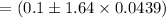
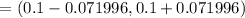
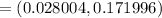
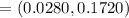
c). Zero is not included in the confidence interval. Answer is no. The difference in the two population proportion are different from each other.