Question

Chapter 07, Problem 065 The drag characteristics of an airplane are to be determined by model tests in a wind tunnel operated at an absolute pressure of 1300 kPa. If the prototype is to cruise in standard air at 406 km/hr, and the corresponding speed of the model is not to differ by more than 29% from this (so that compressibility effects may be ignored), what range of length scales may be used if Reynolds number similarity is to be maintained? Assume the viscosity of air is unaffected by pressure, and the temperature of air in the tunnel is equal to the temperature of the air in which the airplane will fly.

Answer 1

the range of length scales is ( 0.0602 - 0.1094 )

Explanation:

Given the data in the question;

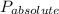`P_{absolute` = 1300 kPa

V
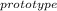`_{prototype` = 406 km/h

speed of model nit more than 29%

we know that Reynolds number Re = pVl/μ = constant

p
`_m`V
`_m`l
`_m`/μ
`_m` = pVl/μ

such that;

l
`_m`/l = ( p/p
`_m` )( V/V
`_m` )( μ
`_m`/μ ) ----- let this be equation 1

Now, for an idea gas; P = pRT { with constant temperature }

p / p = constant; p/p
`_m` = p/p
`_m`

assuming μ
`_m` = μ
`_m`

Therefore, the relation becomes;

l
`_m`/l = ( p/p
`_m` )( V/V
`_m` )

from the given data;

l
`_m`/l = ( 101/1300 )( V/V
`_m` )

where our V
`_m` = ( 1 ± 29% )V

so

l
`_m`/l = ( 101/1300 )( V / ( 1 ± 29% )V )

l
`_m`/l = ( 101/1300 )( 1 / ( 1 ± 0.29 ) )

Now, The minimum limit will be;

l
`_m`/l = ( 101/1300 )( 1 / ( 1 + 0.29 ) )

= ( 101/1300 ) × ( 1 / 1.29 )

= 0.0602

The maximum limit will be;

l
`_m`/l = ( 101/1300 )( 1 / ( 1 - 0.29 ) )

= ( 101/1300 ) × ( 1 / 0.71 )

= 0.1094

Therefore, the range of length scales is ( 0.0602 - 0.1094 )