Answer:
Step-by-step explanation:
Initially no of atoms of A = N₀(A)
Initially no of atoms of B = N₀(B)
5 X N₀(A) = N₀(B)
N = N₀
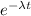
N is no of atoms after time t , λ is decay constant and t is time .
For A
N(A) = N(A)₀

For B
N(B) = N(B)₀
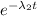
N(A) = N(B) , for t = 2 h
N(A)₀
 = N(B)₀
= N(B)₀
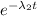
N(A)₀
 = 5 x N₀(A)
= 5 x N₀(A)
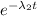
 = 5
= 5
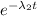
 = 5
= 5
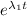
half life = .693 / λ
For A
.77 = .693 / λ₁
λ₁ = .9 h⁻¹
 = 5
= 5
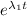
Putting t = 2 h , λ₁ = .9 h⁻¹
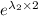 = 5
= 5
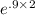
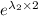 = 30.25
= 30.25
2 x λ₂ = 3.41
λ₂ = 1.7047
Half life of B = .693 / 1.7047
= .4065 hours .
= .41 hours .