Question

A horticulturist working for a large plant nursery is conducting experiments on the growth rate of a new shrub. Based on previous research, the horticulturist feels the average weekly growth rate of the new shrub is 4cm per week. A random sample of 40 shrubs has an average growth of 1.50cm per week with a standard deviation of 5cm. Is there overwhelming evidence to support the claim that the growth rate of the new shrub is less than 4cm per week at a 0.200 significance level?

Find the value of the test statistic. Round your answer to three decimal places, if necessary.

Answer 1

Following are the answer to the given question:

Explanation:

Following are the null and alternative Hypothesis:

`Null \ Hypothesis: \mu = 4\\\\Alternative \ Hypothesis: \mu < 4`

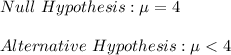
Rejection Zone

This is left tailed test, for α = 0.2 and df = 39

`critical\ value(t) = -0.851\\\\reject\ H_0 \ when = t < -0.851`

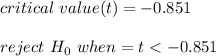
Testing statistic:

`t = \frac{(\bar{x} - \mu)}{( (s)/(√(n)))}`

`= (1.5 - 4)/((5)/(√(40)))\\\\= (-2.5)/((5)/(6.32))\\\\= (-2.5)/(0.79)\\\\ = -3.162`

`P-value = 0.0015`

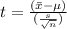
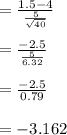
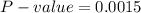
P-value < 0.2, reject the null hypothesis.

Approach to the Rejection Zone:

The null hypothesis is rejected since the test statistic t is outside of the critical range value. Only at the 0.200 significance mark, there's significant evidence that its new shrub's growth rate is less than 4 cm per week.