Question

A tennis player hits a ball 3 feet above the ground with a velocity of 60 ft/sec. After how many seconds will the ball be at a height of 3 feet again?

Answer 1

The ball will be at a height of 3 feet above the ground after 3.729 seconds.

Explanation:

Let suppose that the tennis player has hit the ball vertically, meaning that ball will experiment a free fall, that is, an uniform accelerated motion due to gravity. The time taken by the ball in terms of its initial velocity (
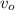`v_(o)`), in feet per second, initial position (
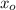`x_(o)`), in feet, final position (
`x`), in feet, and gravitational acceleration (
`g`), in feet per square second is described by this second order polynomial:

`x = x_(o) + v_(o)\cdot t + (1)/(2)\cdot g\cdot t^(2)` (1)

If we know that
`x_(o) = x = 3\,ft`,
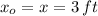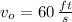`v_(o) = 60\,(ft)/(s)` and
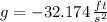`g = -32.174\,(ft)/(s^(2))`, then the time needed by the ball to be at a height of 3 feet again is:

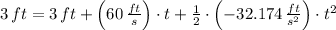
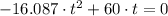`3\,ft = 3\,ft + \left(60\,(ft)/(s) \right)\cdot t + (1)/(2)\cdot \left(-32.174\,(ft)/(s^(2)) \right)\cdot t^(2)`

`-16.087\cdot t^(2)+60\cdot t = 0` (2)

`t^(2) - 3.729\cdot t = 0`

`t \cdot (t -3.729) = 0`

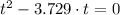
The binomial contains the time when the ball will be at a height of 3 feet again. In other words, the ball will be at a height of 3 feet above the ground after 3.729 seconds.