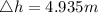Answer:
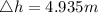
Step-by-step explanation:
From the question we are told that:
Liquid density
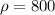
Diameter of pipe

Diameter of venture
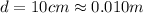
Specific weight of mercury P_mg
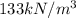
Flow rate
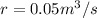
Area A:

Generally the Bernoulli's equation is mathematically given by
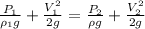
Where
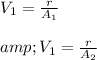
Therefore
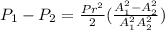
Generally the equation for pressure difference b/w manometer fluid is given as
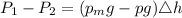
Therefore
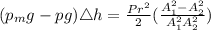
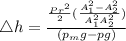
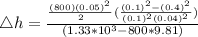
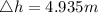
Therefore elevation change is mathematically given by