Answer:
2,304 years old
Explanation:
Given: Jennifer age = 18, Invested = $1000 at 8% interest
To find: How old would she be when the account is $128,000?
Wrong solution
Solution: To figure out how old she will be when her account is $128,000, simply find the difference between her current account value by her current age, by dividing. Then multiply the result by the future account value.
Step 1:
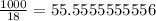
Rounding, that is; 55.56
Step 2: Now, multiply the result by the future account value.
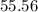 ×
×
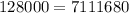
Correct solution
Solution: To find out how old she will be when her account is $128,000, set up a fraction;

Step 1: Divide the numbers

Step 2: Multiply all terms by the same value to eliminate fraction denominators
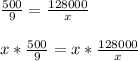
Step 3: Cancel multiplied terms that are in the denominator
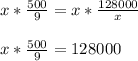
Step 4: Re-order terms so constants are on the left
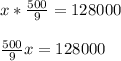
Step 5: Combine multiplied terms into a single fraction
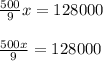
Step 6: Multiply all terms by the same value to eliminate fraction denominators
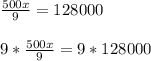
Step 7: Cancel multiplied terms that are in the denominator
[tex]9 * \frac{500x}{9} = 9 * 128000\\500