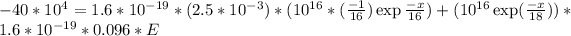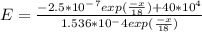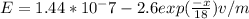Question

The electron concentration in silicon at T = 300 K is given by

n(x) = 10^16exp(-x/18) cm^-3
where x is measured in μm and is limited to 0 ≤ x ≤ 25 μm. The electron diffusion coefficient is Dn = 25 cm2/s and the electron mobility is μn = 960 cm2/V-s. The total electron current density through the semiconductor is constant and equal to Jn = -40 A/cm2. The electron current has both diffusion and drift current components. Determine the electric field as a function of x which must exist in the semiconductor.

Answer 1

`E=1.44*10^-7-2.6exp((-x)/(18) )v/m`

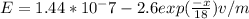
Step-by-step explanation:

From the question we are told that:

Temperature of silicon
`T=300k`

Electron concentration
`n(x)=10^(16)\exp ((-x)/(18))`

`(dn)/(dx)=(10^(16) *((-1)/(16))\exp(-x)/(16))`

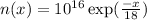
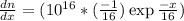
Electron diffusion coefficient is
`Dn = 25cm^2/s \approx 2.5*10^(-3)`

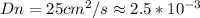
Electron mobility is
`\mu n = 960 cm^2/V-s \approx0.096m/V`

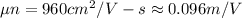
Electron current density
`Jn = -40 A/cm^2 \approx -40*10^(4)A/m^2`

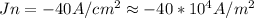
Generally the equation for the semiconductor is mathematically given by

`Jn=qb_n(dn)/(dx)+nq \mu E`

Therefore

`-40*10^(4)=1.6*10^(-19) *(2.5*10^(-3))*(10^(16) *((-1)/(16))\exp(-x)/(16))+(10^(16)\exp ((-x)/(18)))*1.6*10^(-19)*0.096* E`

`E=(-2.5*10^-^7 exp((-x)/(18))+40*10^(4))/(1.536*10^-4exp((-x)/(18) ))`

`E=1.44*10^-7-2.6exp((-x)/(18) )v/m`