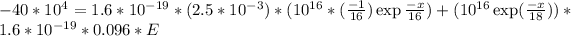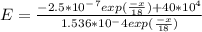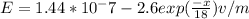Answer:
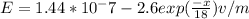
Step-by-step explanation:
From the question we are told that:
Temperature of silicon
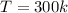
Electron concentration
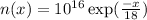
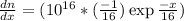
Electron diffusion coefficient is
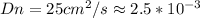
Electron mobility is
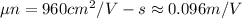
Electron current density
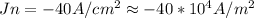
Generally the equation for the semiconductor is mathematically given by
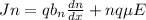
Therefore