Answer:
(a): y increases on average by 8.63/unit of x1 in the first equation and increases on average by 9.01/unit of x1 in the second
(b): Yes
Explanation:
Given
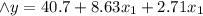

Solving (a): An interpretation of x1 coefficient
We have the coefficients of x1 to be 8.63 and 9.01
Literally, the coefficient represents the average change of y-variable per unit increase of the dependent variable
Since the coefficients of x1 in both equations are positive, then that represents an increment on the y variable.
So, the interpretation is:
y increases on average by 8.63/unit of x1 in the first equation and increases on average by 9.01/unit of x1 in the second
Solving (b): Multicollinearity
This could be the cause because x1 and x2 are related and as a result, x2 could take a part of the coefficient of x2