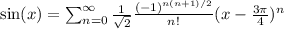Answer:
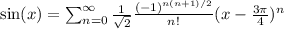
Explanation:
Given
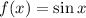
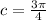
Required
Find the Taylor series
The Taylor series of a function is defines as:
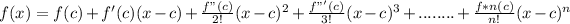
We have:
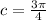
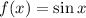

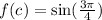
This gives:
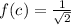
We have:
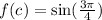
Differentiate
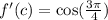
This gives:
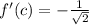
We have:
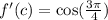
Differentiate
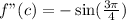
This gives:
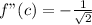
We have:
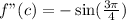
Differentiate
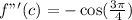
This gives:
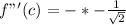
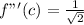
So, we have:
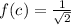
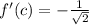
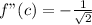
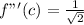
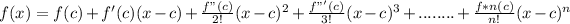
becomes
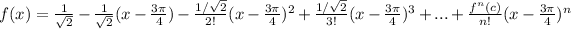
Rewrite as:

Generally, the expression becomes
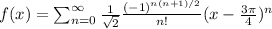
Hence: