Question

The quadratic functions f(x) and g(x) are described as follows:

f(x) = −8x2 + 7


x g(x)
0 0
1 2
2 6
3 2
4 0


Which of the following statements best compares the maximum value of the two functions?
The maximum value is the same for both functions.
f(x) has a greater maximum value than g(x).
g(x) has a greater maximum value than f(x).
The maximum values cannot be determined.

Answer 1

Answer: the other answer is wrong the right one is

f(x) has a greater maximum value than g(x).

Explanation:

Answer 2

Given:

f(x) and g(x) are two quadratic functions.

`f(x)=-8x^2-7`

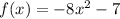
The table of values for the function g(x) is given.

To find:

The statement that best compares the maximum value of the two functions.

Solution:

We have,

`f(x)=-8x^2-7`

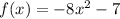
Here, the leading coefficient is -8 which is a negative number. So, the function f(x) represents a downward parabola.

We know that the vertex of a downward parabola is the point of maxima.

The vertex of a quadratic function
`f(x)=ax^2+bx+c` is:

`Vertex=\left((-b)/(2a),f(-(b)/(2a))\right)`

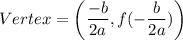
In the given function,
`a=-8,b=0,c=-7`.

`-(b)/(2a)=-(0)/(2(-8))`

`-(b)/(2a)=0`

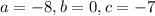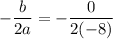
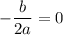
Putting
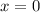`x=0` in the given function, we get

`f(0)=-8(0)^2-7`

`f(0)=-7`

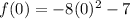
So, the vertex of the function f(x) is at (0,-7). It means the maximum value of the function f(x) is -7.

From the table of g(x) it is clear that the maximum value of the function g(x) is 6.

Since
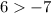`6>-7`, therefore g(x) has a greater maximum value than f(x).

Hence, the correct option is C.