We are given that , in a right angled triangle the hypotenuse is 8 units and it's one leg is 5 units . And we need to find the another leg . So , here Pythagoras theorem will be very helpful for us which states that in any Right Triangle , the sum of square of it's two sides ( base and perpendicular or two legs ) is equal to the square of it's largest side ( Hypotenuse )
Now , let's assume that the other leg be x , so now by Pythagoras theorem ;
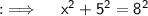
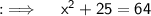
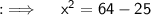
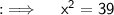
Raising power to ½ on both sides will leave us with x = +√39 , -√39. But as length can never be -ve

Hence , the another leg of the right angled triangle is √39 units