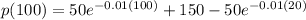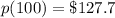Answer:
~
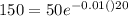
~
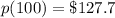
Explanation:
From the question we are told that:
Price of 20TVs per week
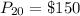
Marginal price-demand function
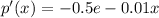
Generally the The Marginal price function is mathematically given by
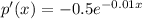
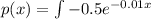
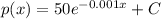
Therefore the equation when the demand is 20 TVs per week at $150 per TV
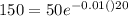
Giving
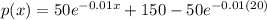
Therefore the Price when the demand is 100 TVs per week