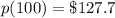Question

Find the price-demand equation for a particular brand television when the demand is 20 TVs per week at $150 per TV, given that the marginal price-demand function, p′(x), for x number of TVs per week, is given as p′(x)=−0.5e−0.01x. If 100 TVs are sold per week, what should the price be? Round your answer to the nearest hundredth and do not include a dollar sign in your answer.

Answer 1

~
`150=50e^(-0.01()20)`

~
`p(100)=\$127.7`

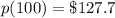
Explanation:

From the question we are told that:

Price of 20TVs per week
`P_(20)=\$150`

Marginal price-demand function
`p'(x)=-0.5e-0.01x`

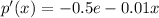
Generally the The Marginal price function is mathematically given by

`p'(x)=-0.5e^(-0.01x)`

`p(x)=\int-0.5e^(-0.01x)`

`p(x)=50e^(-0.001x)+C`

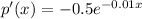
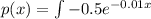
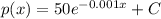
Therefore the equation when the demand is 20 TVs per week at $150 per TV

`150=50e^(-0.01()20)`

Giving

`p(x)=50e^(-0.01x)+150-50e^(-0.01(20))`

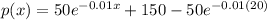
Therefore the Price when the demand is 100 TVs per week

`p(100)=50e^(-0.01(100))+150-50e^(-0.01(20))`

`p(100)=\$127.7`