Question

Determine the magnitude and direction of the resultant force of the following free body diagram.

Answer 1

The magnitude and direction of the resultant force are approximately 599.923 newtons and 36.405°.

Step-by-step explanation:

First, we must calculate the resultant force (
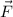`\vec F`), in newtons, by vectorial sum:

`\vec F = [(-200\,N)\cdot \cos 60^(\circ)+(400\,N)\cdot \cos 45^(\circ)+300\,N]\,\hat{i} + [(200\,N)\cdot \sin 60^(\circ) + (400\,N)\cdot \sin 45^(\circ)-100\,N]\,\hat{j}` (1)

`\vec F = 182.843\,\hat{i} + 356.048\,\hat{j}`

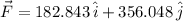
Second, we calculate the magnitude of the resultant force by Pythagorean Theorem:

`\|\vec F\| = \sqrt{(482.843\,N)^(2)+(356.048\,N)^(2)}`

`\|\vec F\| \approx 599.923\,N`

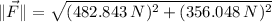
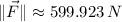
Let suppose that direction of the resultant force is an standard angle. According to (1), the resultant force is set in the first quadrant:

`\theta = \tan^(-1)\left((356.048\,N)/(482.843\,N) \right)`

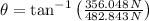
Where
`\theta` is the direction of the resultant force, in sexagesimal degrees.

`\theta \approx 36.405^(\circ)`

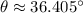
The magnitude and direction of the resultant force are approximately 599.923 newtons and 36.405°.