Answer:
pH = 3.215
Step-by-step explanation:
From the given information;
Using the equation for the dilution of a stock solution:
Since moles of C5H5N = moles of HNO3
Then:
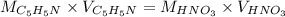
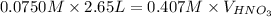
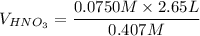
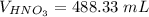
The reaction between C5H5NH and H2O is as follows:
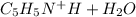 ⇄
⇄
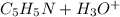
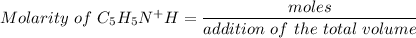
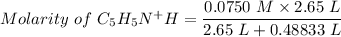
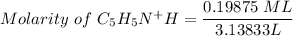
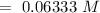
Now, the next step is to draw out the I.C.E table.
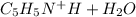 ⇄
⇄
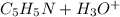
I 0.06333 0 0
C - x x x
E 0.06333 -x x x
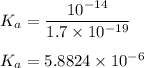
![K_a = ([C_5H_5N][H_3O^+] )/([C_5H_5N^+H] ) \\ \\ 5.8824 * 10^(-6) = (x^2)/(0.06333 - x)](https://img.qammunity.org/2022/formulas/biology/college/gl69q5sarpeg90t6rsby8sxprgmkmx5rzd.png)
Assuming x < 0.06333
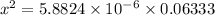
Then
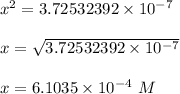
![[H_3O^+] = x = 6.1035 * 10^(-4) \ M \\ \\ pH = -log (6.1035 * 10^(-4)) \\ \\ \mathbf{\\ pH = 3.215}](https://img.qammunity.org/2022/formulas/biology/college/he77lsccubzmr3suhnekmw2r275dp6909l.png)