Question

Bob and Anna are planning to meet for lunch at Sally's Restaurant, but they forgot to schedule a time. Bob and Anna are each going to randomly choose from either 1\text{ p.m.}1 p.m.1, start text, space, p, point, m, point, end text, 2\text{ p.m.}2 p.m.2, start text, space, p, point, m, point, end text, 3\text{ p.m.}3 p.m.3, start text, space, p, point, m, point, end text, or 4\text{ p.m.}4 p.m.4, start text, space, p, point, m, point, end text to show up at Sally's Restaurant. They must both choose exactly the same time in order to meet. Bob has a "buy one entree, get one entree free" coupon that he can only use if he meets up with Anna. If he successfully meets with Anna, Bob's lunch will cost him \$5$5dollar sign, 5. If they do not meet, Bob's lunch will cost him \$10$10dollar sign, 10. What is the expected cost of Bob's lunch?

Answer 1

The expected cost is $8.75

Explanation:

Given

`Time = \{1pm, 2pm, 3pm, 4pm\}`

`C_1 = \$5` --- If Bob and Anna meet

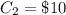`C_2 = \$10` --- If Bob and Anna do not meet

Required

The expected cost of Bob's meal

First, we list out all possible time both Bob and Anna can select

We have:

`(Bob,Anna) = \{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3)`
`,(3,4),(4,1),(4,2),(4,3),(4,4)\}`

`n(Bob, Anna) = 16`

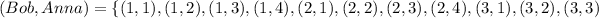
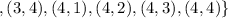
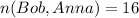
The outcome of them meeting at the same time is:

`Same\ Time = \{(1,1),(2,2),(3,3),(4,4)\}`

`n(Same\ Time) = 4`

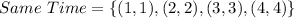
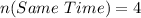
The probability of them meeting at the same time is:

`Pr(Same\ Time) = (n(Same\ Time))/(n(Bob,Anna))`

`Pr(Same\ Time) = (4)/(16)`

`Pr(Same\ Time) = (1)/(4)`

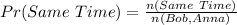
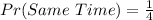
The outcome of them not meeting:

`Different = \(Bob,Anna) = \{(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2)`

`,(3,4),(4,1),(4,2),(4,3)\}`

`n(Different) = 12`

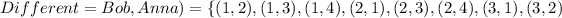
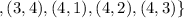
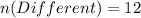
The probability of them meeting at the same time is:

`Pr(Different) = (n(Different))/(n(Bob,Anna))`

`Pr(Different) = (12)/(16)`

`Pr(Different) = (3)/(4)`

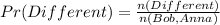
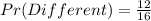
The expected cost is then calculated as:

`Expected = C_1 * P(Same) + C_2 * P(Different)`

`Expected = \$5 * (1)/(4) + \$10 * (3)/(4)`

`Expected = (\$5)/(4) + (\$30)/(4)`

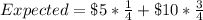
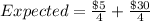
Take LCM

`Expected = (\$5+\$30)/(4)`

`Expected = (\$35)/(4)`

`Expected = \$8.75`

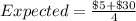
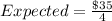
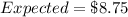
The expected cost is $8.75