Answer:
The pvalue of the test is 0.0012 < 0.05, which means that the data provides convincing evidence that the pediatrician's claim is true.
Explanation:
A pediatrician claims that the mean weight of one-year-old boys is greater than 25 pounds.
This means that at the null hypothesis, we test that the mean is 25 pounds, that is:
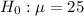
At the alternate hypothesis, we test that it is more than 25 pounds, that is:
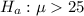
The test statistic is:
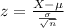
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
25 is tested at the null hypothesis:
This means that
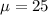
The National Health Statistics Reports described a study in which a sample of 315 one-year-old baby boys were weighed. Their mean weight was 25.6 pounds with standard deviation 5.3 pounds.
This means that
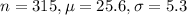
Value of the test-statistic:
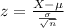
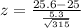
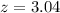
Pvalue of the test and decision:
The pvalue of the test is the probability of finding a mean above 25.6 pounds, which is 1 subtracred by the pvalue of z = 3.04.
Looking at the z-table, z = 3.04 has a pvalue of 0.9988
1 - 0.9988 = 0.0012
The pvalue of the test is 0.0012 < 0.05, which means that the data provides convincing evidence that the pediatrician's claim is true.