Question

Big babies: The National Health Statistics Reports described a study in which a sample of 315 one-year-old baby boys were weighed. Their mean weight was 25.6 pounds with standard deviation 5.3 pounds. A pediatrician claims that the mean weight of one-year-old boys is greater than 25 pounds. Do the data provide convincing evidence that the pediatrician's claim is true? Use the =α0.05 level of significance and the critical value method with the

Answer 1

The pvalue of the test is 0.0012 < 0.05, which means that the data provides convincing evidence that the pediatrician's claim is true.

Explanation:

A pediatrician claims that the mean weight of one-year-old boys is greater than 25 pounds.

This means that at the null hypothesis, we test that the mean is 25 pounds, that is:

`H_0: \mu = 25`

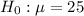
At the alternate hypothesis, we test that it is more than 25 pounds, that is:

`H_a: \mu > 25`

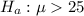
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

25 is tested at the null hypothesis:

This means that
`\mu = 25`

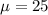
The National Health Statistics Reports described a study in which a sample of 315 one-year-old baby boys were weighed. Their mean weight was 25.6 pounds with standard deviation 5.3 pounds.

This means that
`n = 315, \mu = 25.6, \sigma = 5.3`

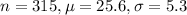
Value of the test-statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (25.6 - 25)/((5.3)/(√(315)))`

`z = 3.04`

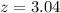
Pvalue of the test and decision:

The pvalue of the test is the probability of finding a mean above 25.6 pounds, which is 1 subtracred by the pvalue of z = 3.04.

Looking at the z-table, z = 3.04 has a pvalue of 0.9988

1 - 0.9988 = 0.0012

The pvalue of the test is 0.0012 < 0.05, which means that the data provides convincing evidence that the pediatrician's claim is true.