Answer:
x = 13°
y = 36°
Explanation:
Given the diagram of vertical angles, such that the sides of two angles form two pairs of opposite rays:
We are also given the following values for the following angles:
∠BMQ = (x + 10)°
∠DME = (3x - 16)°
∠EMQ = (5y - x - 10)°
According to the Vertical Angles Congruence Theorem, vertical angles are congruent.
In the given diagram, the following are vertical angles:
∠BMQ and ∠DME
∠BMD and ∠QME
Thus, in reference to the Vertical Angles Congruence Theorem, we can establish the following equality statement to solve for the value of x:
∠BMQ = ∠DME
(x + 10)° = (3x - 16)°
Solve for x:
We can proceed to solve for the value of x. Start by adding 16° to both sides:
x° + 10° + 16° = 3x° - 16° + 16°
x° + 26° = 3x°
Next, subtract x° from both sides:
x° - x° + 26° = 3x° - x°
26° = 2x°
Divide both sides by 2° to solve for x:
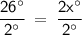
x = 13°
Solve for y:
By definition, linear pairs are two adjacent angles whose noncommon sides are the opposite rays. Linear pairs are also supplementary angles whose measures add up to 180°.
In the given diagram, the following angles are linear pairs:
∠DME and ∠EMQ
∠EMQ and ∠QMB
∠QMB and ∠BMD
∠BMD and ∠DME
Using the given value for ∠DME and ∠EMQ, we can solve for the value of y by setting up the following equation:
m∠DME + m∠EMQ = 180° ⇒ By definition of Linear Pairs.
(3x - 16)° + (5y - x - 10)° = 180°
Substitute the value of x into the equation:
3(13)° - 16° + 5y° - 13° - 10° = 180°
Combine like terms:
39° - 16° + 5y° - 13° - 10° = 180°
0° + 5y° = 180°
5y° = 180°
Divide both sides by 5 to solve for y:
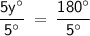
y = 36°
Double-check:
Verify whether we have the correct values for x and y by substituting their values into each angle:
Verify: ∠BMQ and ∠DME are vertical angles with the same measure:
∠BMQ = (x + 10)° = 13° + 10° = 23°
∠DME = (3x - 16)° = 3(13)° - 16° = 23°
⇒ True statement.
m∠DME + m∠EMQ = 180° ⇒ By definition of Linear Pairs.
∠DME = 23°
∠EMQ = (5y - x - 10)° = [5(36) - 13 - 10]° = 180 - 23 = 157°
23° + 157° = 180°
180° = 180° (True statement).