This question is incomplete, the complete question is;
The times when goals are scored in hockey are modeled as a Poisson process in Morrison (1976). For such a process, assume that the average time between goals is 15 minutes.
(The parameter of the hockey Poisson Process is lambda = 1/15 )
(i) In a 60-minute game, find the probability that a fourth goal occurs in the last 5 minutes of the game?
(ii) Assume that at least three goals are scored in a game. What is the mean time of the third goal?
Answer:
i) the probability that a fourth goal occurs in the last 5 minutes of the game is 0.068
ii) The mean time of the third goal is 33.5 minutes
Explanation:
Given the data in the question;
The parameter of the hockey Poisson Process λ = 1/15
i)
Let us represent the probability of a fourth goal in the last 5 min in a 60 min game with X.
Thus, we find the probability that X is greater than ( 60min - 5min) and less than or equal to 60min
so;
p( 55 < X ≤ 60 ) =
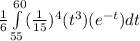
p( 55 < X ≤ 60 ) = 0.06766 ≈ 0.068
Therefore, the probability that a fourth goal occurs in the last 5 minutes of the game is 0.068
ii)
Also let us represent the probability that at least 3 goals are scored in the game with X
Now, the mean time of the third goal will be;
P(X|X < 60 ) =
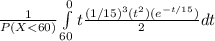
P(X|X < 60 ) = 25.49 / 0.76
P(X|X < 60 ) = 33.539 ≈ 33.5
Therefore, the mean time of the third goal is 33.5 minutes