Question

The time it takes students in a cooking school to learn how to prepare a particular meal is a random variable with a mean of 3.2 hours and a standard deviation of 1.9 hours. Find the probability that the average time it will take 38 students to learn how to prepare the meal a) is less than 3.4 hours (Draw the bell curve) 4 b) is between 3.0 hours and 3.6 hours (Draw the bell curve)

Answer 1

Explanation:

From the given information:

Mean
`\mu` = 3.2

Standard deviation
`\sigma` = 1.9

sample size n = 38

Mean of sampling distribution
`\mu _(\bar x) = \mu = 3.2`

Standard deviation of the sample mean is:

`\sigma _(\bar x) = (\sigma)/(√(n)) \\ \\ = (1.9)/(√(38)) \\ \\ = 0.3082`

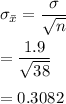
a)

To find P(x < 3.4)

`= P\Big( ((\bar x - \mu_(\bar x) ) )/(\sigma_(\bar x)) < (3.4 - 3.2)/(0.3082)\ \Big)`

`= P\Big( Z< (0.2)/(0.3082)\ \Big) \\ \\= P\Big( Z< 0.65 \ \Big)`

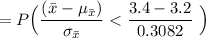
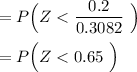
Using the standard normal table

`P(z < 0.65) = 0.7422`

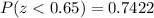
The Bell curved shape is attached in the diagram below.

b)

To find P(3 < x < 3.6)

`= P\Big( (3.0-3.2)/(0.3082) < ((\bar x - \mu_(\bar x) ) )/(\sigma_(\bar x)) < (3.6 - 3.2)/(0.3082)\ \Big)`

`= P\Big( (-0.2)/(0.3082) < ((\bar x - \mu_(\bar x) ) )/(\sigma_(\bar x)) < (0.4)/(0.3082)\ \Big)`

`= P (-0.65 < Z < 1.30)`

`= P(Z < 1.30) - P(Z < -0.65)`

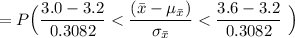
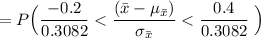
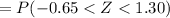
Using the standard normal table

= 0.9032 -0.2578

=0.6454