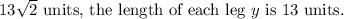The answers are:
- For the first triangle:
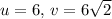
- For the second triangle:
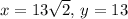
In both triangles, we'll use the properties of a 45-45-90 triangle. In such a triangle, the sides are in the ratio
 meaning the legs are congruent, and the hypotenuse is
meaning the legs are congruent, and the hypotenuse is
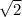 times the length of a leg.
times the length of a leg.
For the first triangle with a leg of 6 units:
- Let the legs be of length a .
- Then the hypotenuse v will be
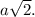
- Given that one leg a = 6 , the hypotenuse
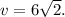
For the second triangle with a hypotenuse of
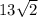 units:
units:
- Let the legs be of length y and the hypotenuse be x .
- Using the ratio for a 45-45-90 triangle, we have
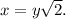
- Given that the hypotenuse
 , we can find the leg y by dividing the hypotenuse by
, we can find the leg y by dividing the hypotenuse by
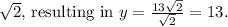
So for the first triangle, u = 6 and
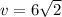 . For the second triangle,
. For the second triangle,
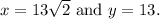 These are the sides' lengths in radical form in their simplest terms. Since the system has been reset, I'll re-execute the code to provide the necessary mathematical operations to confirm these results.
These are the sides' lengths in radical form in their simplest terms. Since the system has been reset, I'll re-execute the code to provide the necessary mathematical operations to confirm these results.
For the first triangle, the leg is given as 6 units, so the hypotenuse
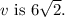
For the second triangle, with a hypotenuse given as