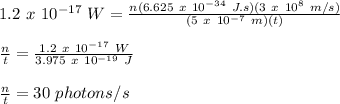Question

Eye at the lowest radiated power of 1,2 x10 x (- 17) W. Determine how many photons of light with a wavelength of 500nm fall on the retina of the eye every second

Answer 1

`(n)/(t) = 30\ photons/s`

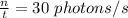
Step-by-step explanation:

The radiated power can be given in terms of the wavelength as follows:

`Rasiated\ Power = (nE)/(t) = (nhc)/(\lambda t)`

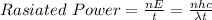
where,

Radiated Power = 1.2 x 10⁻¹⁷ W

n = no. of photons = ?

h = plank's constant = 6.625 x 10⁻³⁴ J.s

c = speed of light = 3 x 10⁸ m/s

λ = wavelength = 500 nm = 5 x 10⁻⁷ m

t = time

Therefore,

`1.2\ x\ 10^(-17)\ W = (n(6.625\ x\ 10^(-34)\ J.s)(3\ x\ 10^8\ m/s))/((5\ x\ 10^(-7)\ m)(t) )\\\\(n)/(t) = (1.2\ x\ 10^(-17)\ W)/(3.975\ x\ 10^(-19)\ J)\\\\(n)/(t) = 30\ photons/s`