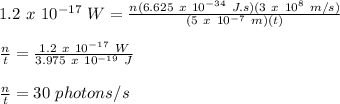Answer:
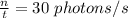
Step-by-step explanation:
The radiated power can be given in terms of the wavelength as follows:
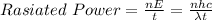
where,
Radiated Power = 1.2 x 10⁻¹⁷ W
n = no. of photons = ?
h = plank's constant = 6.625 x 10⁻³⁴ J.s
c = speed of light = 3 x 10⁸ m/s
λ = wavelength = 500 nm = 5 x 10⁻⁷ m
t = time
Therefore,