Question

Simplify the sum plz

Answer 1

`\Huge\boxed{ \bf \frac{ {b}^(2) + {a}^(2) }{ {a}^(3)b }}`

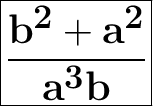
Explanation:

Given expression:

`\sf \longmapsto \frac{ {a}^(3) {b}^(5) }{b {}^(4) {a}^(6) } + \frac{ {a}^(8) {b}^(6) }{b {}^(7) a {}^(9) }`

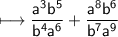
Solution:

`\sf \longmapsto \frac{ {a}^(3) {b}^(5) }{b {}^(4) {a}^(6) } + \frac{ {a}^(8) {b}^(6) }{b {}^(7) a {}^(9) }`

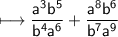
Cancel a^3 and a^6 on the left hand side of plus sign, which results to a^3.

`\sf \longmapsto\frac{ \cancel{{a}^(3)} {b}^(5) }{b {}^(4) \cancel{{a}^(6)} } + \frac{ {a}^(8) {b}^(6) }{b {}^(7) a {}^(9) }`

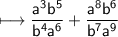
That is,

`\sf \longmapsto \frac{b {}^(5) }{b {}^(4) a {}^(3) } + \frac{ {a}^(8) {b}^(6) }{b {}^(7) a {}^(9) }`

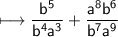
Cancel b^5 and 5^4 on the LHS of plus sign, which results to b.

`\sf \longmapsto \frac {\cancel{b {}^(5) }}{ \cancel{b {}^(4)} a {}^(3) } + \frac{ {a}^(8) {b}^(6) }{b {}^(7) a {}^(9) }`

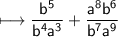
That is,

`\sf \longmapsto \frac{b }{ a {}^(3) } + \frac{ {a}^(8) {b}^(6) }{b {}^(7) a {}^(9) }`

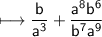
Now cancel a^8 and a^9 on the RHS of Plus sign, which results to a.

`\sf \longmapsto\frac{b }{ a {}^(3) } + \frac{ \cancel{{a}^(8)} {b}^(6) }{b {}^(7) \cancel{a {}^(9)} }`

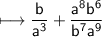
That is,

`\sf \longmapsto \: \frac{b }{ a {}^(3) } + \frac{ {b}^(6) }{b {}^(7) a {}^{} }`

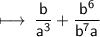
Cancel b^6 and b^7 on the RHS of the Plus sign, which results to b.

`\sf \longmapsto\frac{b }{ a {}^(3) } + \frac{ \cancel{ {b}^(6)} }{ \cancel{b {}^(7)} a {}^{} }`

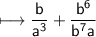
That is,

`\sf \longmapsto\frac{b }{ a {}^(3) } + \cfrac {1}{ {b {}^(1)} a {}^{} }`

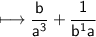
Simply add:-

Rewrite into:

`\sf \longmapsto \: \frac{ b {}^{} }{a {}^(3) } + \cfrac{1}{a * b}`

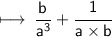
Combine the numerators over LCD(a^3)

`\sf \longmapsto \: \frac{ {b}^(2) + {a}^(2) }{ {a}^(3)b }`

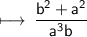
Or it can also be rewritten as,

`\sf \longmapsto \: \frac{ {a}^(2) + {b}^(2) }{ {a}^(3)b }`

________________________________

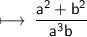
I hope this helps!

Please let me know if you have any questions

Answer 2

• (a² + b²)/a³b

Explanation:

Simplify the given expression:

• a³b⁵/b⁴a⁶ + a⁸b⁶/b⁷a⁹

The first fraction simplifies as:

• b/a³ by cancelling a³ and b⁴

The second fraction simplifies as:

• 1/ab by cancelling a⁸ and b⁶

The sum becomes:

• b/a³ + 1/ab = Common denominator is a³b
• b²/a³b + a²/a³b = Multiply the first fraction by b, the second by a²
• (a² + b²)/a³b