Answer:
No
Explanation:
Given the following question
In order to prove if three lengths can create a triangle two of the three sides added together HAS to be greater than the third side.
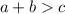
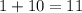
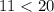
Which means your answer is "no," the given sides cannot create a triangle for they do not pass the Triangle Inequality Theorem.
Hope this helps.