Question

Twenty nine concrete blocks were sampled and tested for crushing strength in order to estimate the proportion that were sufficiently strong for a certain application. Twenty seven of the 29 blocks were sufficiently strong. Use the small-sample method to construct a 95% confidence interval for the proportion of blocks that are sufficiently strong.

Answer 1

95% confidence interval for the proportion of blocks that are sufficiently strong

(0.83913 , 1.02293)

Explanation:

Step:-1

Given that the sample size 'n' = 29 blocks

Estimate proportion

`p = (x)/(n) = (27)/(29) = 0.93103`

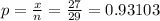
Step:-2

95% confidence interval for the proportion of blocks that are sufficiently strong

`(p^(-) -Z_(0.05) \sqrt{(p(1-p))/(n) } , p^(-) + Z_(0.05) \sqrt{(p(1-p))/(n) } )`

`(0.93103 -1.96 \sqrt{(0.93103(1-0.93103))/(29) } , 0.93103 + 1.96 \sqrt{(0.93103(1-0.93103))/(29) } )`

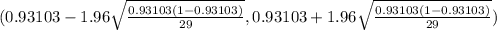
(0.93103 - 0.0919 , 0.93103 +0.0919)

(0.83913 , 1.02293)

Final answer:-

95% confidence interval for the proportion of blocks that are sufficiently strong

(0.83913 , 1.02293)