Answer:
95% confidence interval for the proportion of blocks that are sufficiently strong
(0.83913 , 1.02293)
Explanation:
Step:-1
Given that the sample size 'n' = 29 blocks
Estimate proportion
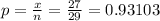
Step:-2
95% confidence interval for the proportion of blocks that are sufficiently strong
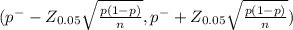
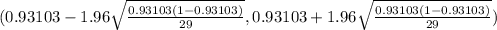
(0.93103 - 0.0919 , 0.93103 +0.0919)
(0.83913 , 1.02293)
Final answer:-
95% confidence interval for the proportion of blocks that are sufficiently strong
(0.83913 , 1.02293)