Answer:
The coordinates of points P', Q' and R' are (-24, 32), (-64, 24) and (-8,-48), respectively.
Explanation:
Vectorially speaking, the dilation of a vector with respect to a given point is defined by the following formula:
![P'(x,y) = O(x,y) + r\cdot [P(x,y)-O(x,y)]](https://img.qammunity.org/2022/formulas/mathematics/college/m5kjgz8o62drjudj2ytc4hf7ydts471yqy.png) ,
,
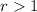 (1)
(1)
Where:
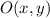 - Point of reference.
- Point of reference.
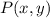 - Original point.
- Original point.
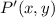 - Dilated point.
- Dilated point.
 - Scale factor.
- Scale factor.
If we know that
 ,
,
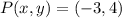 ,
,
 ,
,
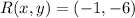 and
and
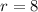 , then the new coordinates of the triangle are, respectively:
, then the new coordinates of the triangle are, respectively:
![P'(x,y) = (0,0) + 8\cdot [(-3,4)-(0,0)]](https://img.qammunity.org/2022/formulas/mathematics/college/ib44rprte4j7ry7mvf2gnwzao8d8ap8xuj.png)
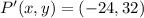
![Q'(x,y) = (0,0) + 8\cdot [(-8,3)-(0,0)]](https://img.qammunity.org/2022/formulas/mathematics/college/224yqy9qupc58u93obk5kqf7k7406sx2d1.png)

![R'(x,y) = (0,0) + 8\cdot [(-1,-6)-(0,0)]](https://img.qammunity.org/2022/formulas/mathematics/college/n91qxcs4hitkdv90umusokhq09xc76j184.png)
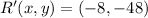
The coordinates of points P', Q' and R' are (-24, 32), (-64, 24) and (-8,-48), respectively.