Answer:
El padre tenía un capital de 60,000 euros.
El hijo mayor recibe 12,000 euros.
El hijo segundo recibe 15,000 euros.
El hijo tercero recibe 33,000 euros.
Explanation:
Sea
 el capital total del padre y
el capital total del padre y
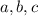 son las asignaciones a los hijos mayor, segundo y tercero. A continuación, construimos las ecuaciones matemáticas a partir de lo descrito en el enunciado:
son las asignaciones a los hijos mayor, segundo y tercero. A continuación, construimos las ecuaciones matemáticas a partir de lo descrito en el enunciado:
Hijo mayor
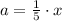 (1)
(1)
Hijo segundo
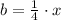 (2)
(2)
Hijo tercero
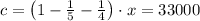 (3)
(3)
De (3) tenemos que el capital del padre es:
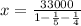
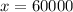
El padre tenía un capital de 60,000 euros.
Por (1) y (2) determinamos los capitales del hijo mayor y el hijo segundo:
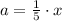
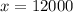
El hijo mayor recibe 12,000 euros.
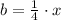
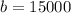
El hijo segundo recibe 15,000 euros.