1 Answer

Anthony Anisimov · Answer 1 · 2022-05-31T23:18:01+0000

Given:

In the given triangle the measure of two angles are 102 degree and 28 degrees and the sides of the triangle are a, 27 cm, c.

To find:

The value of a.

Solution:

Let the given triangle be ABC, such that,

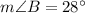
$m\angle B=28^\circ$

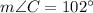
$m\angle C=102^\circ$

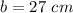
$b=27\ cm$

Using angle sum property of triangles, we get

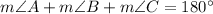
$m\angle A+m\angle B+m\angle C=180^\circ$

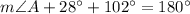
$m\angle A+28^\circ+102^\circ=180^\circ$

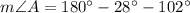
$m\angle A=180^\circ-28^\circ-102^\circ$

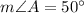
$m\angle A=50^\circ$

According to the Law of Sines:

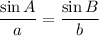
$(\sin A)/(a)=(\sin B)/(b)$

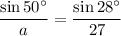
$(\sin 50^\circ )/(a)=(\sin 28^\circ )/(27)$

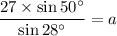
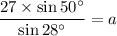
$(27* \sin 50^\circ )/(\sin 28^\circ)=a$

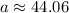
$a\approx 44.06$

Therefore, the value of a is about 44.06 cm.

Please log in or register to add a comment.