Question

The two triangles are similar. Determine the values of x, y, and z.

Answer 1

y= 20 m

x= 15 m

z= 22 degree

Explanation:

15+x=30 m

x=30-15

x= 15 m

z-18=40

z= 40-18

z= 22m

Answer 2

The values of x,y and z are as follows:
`(x = 25)(y = 15)(z = 58^\circ)`

To find the values of x, y, and z, we can use the properties of similar triangles.

Let's denote the corresponding sides and angles of triangles XYZ and RQS:

Corresponding sides: (XW = 15 + x, WY = 32, XY = 20) (from triangle XYZ) and (RQ = 30, QS = 24, RS = y) (from triangle RQS).

Corresponding angle:
`(W = 40^\circ)` (from triangle XYZ) and
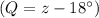`(Q = z - 18^\circ)` (from triangle RQS).

Now, for similar triangles, the corresponding sides are proportional, and the corresponding angles are equal. We can set up the following ratios:For sides:

`[ (XW)/(RQ) = (WY)/(QS) = (XY)/(RS) ]`

Substituting the given values:
`[ (15 + x)/(30) = (32)/(24) = (20)/(y) ]`

For angles:
`[ \angle W = \angle Q \implies 40^\circ = z - 18^\circ ]`

Now, you can solve these equations to find the values of x, y, and z.

Setting up the ratio for sides:
`[ (XW)/(RQ) = (WY)/(QS) = (XY)/(RS) ]`

Substituting the given values:
`[ (15 + x)/(30) = (32)/(24) = (20)/(y) ]`

Simplifying the ratios:
`[ (1)/(2) + (x)/(30) = (4)/(3) \implies (x)/(30) = (4)/(3) - (1)/(2) ]`

Solving for x:
`[ (x)/(30) = (5)/(6) \implies x = 25 ]`

So, (x = 25).

Setting up the equation for angles:
`[ \angle W = \angle Q \implies 40^\circ = z - 18^\circ ]`

Solving .for z:
`[ z = 40^\circ + 18^\circ = 58^\circ ]So, (z = 58^\circ)`

Substituting the value of x into the side ratio equation:
`[ (15 + x)/(30) = (32)/(24) = (20)/(y) ]`Substituting (x = 25):
`[ (15 + 25)/(30) = (40)/(30) = (4)/(3) = (20)/(y) ]`

Solving for y:
`[ (20)/(y) = (4)/(3) \implies y = 15 ]` So, (y = 15).