The values of x,y and z are as follows:
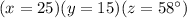
To find the values of x, y, and z, we can use the properties of similar triangles.
Let's denote the corresponding sides and angles of triangles XYZ and RQS:
Corresponding sides: (XW = 15 + x, WY = 32, XY = 20) (from triangle XYZ) and (RQ = 30, QS = 24, RS = y) (from triangle RQS).
Corresponding angle:
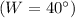 (from triangle XYZ) and
(from triangle XYZ) and
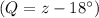 (from triangle RQS).
(from triangle RQS).
Now, for similar triangles, the corresponding sides are proportional, and the corresponding angles are equal. We can set up the following ratios:For sides:
![[ (XW)/(RQ) = (WY)/(QS) = (XY)/(RS) ]](https://img.qammunity.org/2022/formulas/mathematics/college/xq96shrox2b81dydvv6aoko8sf2jg17lhy.png)
Substituting the given values:
![[ (15 + x)/(30) = (32)/(24) = (20)/(y) ]](https://img.qammunity.org/2022/formulas/mathematics/college/htxm8ew18ex0vy0alwak74qjxkjnclm1zu.png)
For angles:
![[ \angle W = \angle Q \implies 40^\circ = z - 18^\circ ]](https://img.qammunity.org/2022/formulas/mathematics/college/kpcz7yahj18mwqvgmfvxh2rr41laaen38y.png)
Now, you can solve these equations to find the values of x, y, and z.
Setting up the ratio for sides:
![[ (XW)/(RQ) = (WY)/(QS) = (XY)/(RS) ]](https://img.qammunity.org/2022/formulas/mathematics/college/xq96shrox2b81dydvv6aoko8sf2jg17lhy.png)
Substituting the given values:
![[ (15 + x)/(30) = (32)/(24) = (20)/(y) ]](https://img.qammunity.org/2022/formulas/mathematics/college/htxm8ew18ex0vy0alwak74qjxkjnclm1zu.png)
Simplifying the ratios:
![[ (1)/(2) + (x)/(30) = (4)/(3) \implies (x)/(30) = (4)/(3) - (1)/(2) ]](https://img.qammunity.org/2022/formulas/mathematics/college/x28pqlbp49rr5xejsviuw4jl4uocavsg3e.png)
Solving for x:
![[ (x)/(30) = (5)/(6) \implies x = 25 ]](https://img.qammunity.org/2022/formulas/mathematics/college/38dnimh769se8q9wrq8oy803bj8dh21arc.png)
So, (x = 25).
Setting up the equation for angles:
![[ \angle W = \angle Q \implies 40^\circ = z - 18^\circ ]](https://img.qammunity.org/2022/formulas/mathematics/college/kpcz7yahj18mwqvgmfvxh2rr41laaen38y.png)
Solving .for z:
![[ z = 40^\circ + 18^\circ = 58^\circ ]So, (z = 58^\circ)](https://img.qammunity.org/2022/formulas/mathematics/college/pqwk68lov05har2ojaeaog7h4r76eyv60e.png)
Substituting the value of x into the side ratio equation:
![[ (15 + x)/(30) = (32)/(24) = (20)/(y) ]](https://img.qammunity.org/2022/formulas/mathematics/college/htxm8ew18ex0vy0alwak74qjxkjnclm1zu.png) Substituting (x = 25):
Substituting (x = 25):
![[ (15 + 25)/(30) = (40)/(30) = (4)/(3) = (20)/(y) ]](https://img.qammunity.org/2022/formulas/mathematics/college/nmgtawnn1krljqngdmxpphx5sxduy2k8ge.png)
Solving for y:
![[ (20)/(y) = (4)/(3) \implies y = 15 ]](https://img.qammunity.org/2022/formulas/mathematics/college/ujtk3pvryex8j16mg57bbi03vbsyb3in35.png) So, (y = 15).
So, (y = 15).