Question

What is the volume of the solid generated when the region in the first quadrant bounded by the graph of y=x^3, the x-axis, and the vertical line x=2 is revolved about the x-axis?

Show work.

A

`4`
B

`(128)/(7)`
C

`4\pi`
D

`(128\pi)/(7)`
​

Answer 1

The first thing we need to do is to find the area bounded by:

y = x^3

y = 0

between:

x = 0 and x = 2

This is the integral of the given function between x = 0 and x = 2, written as:

`\int\limits^2_0 {x^3} \, dx = (2^4)/(4) - (0^4)/(4) = 2^2 = 4`

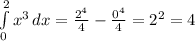
This means that the area of the bounded region is 4 square units.

Now, if we do a full rotation around the x-axis, the volume generated will be equal to the area that we obtained times 2*pi units.

The volume is:

V = (4 square units)*(2*pi units) = 8*pi cubic units.

(Notice that no option coincides with this, there may be a mistake in the options)