Answer:
The first thing we need to do is to find the area bounded by:
y = x^3
y = 0
between:
x = 0 and x = 2
This is the integral of the given function between x = 0 and x = 2, written as:
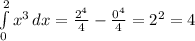
This means that the area of the bounded region is 4 square units.
Now, if we do a full rotation around the x-axis, the volume generated will be equal to the area that we obtained times 2*pi units.
The volume is:
V = (4 square units)*(2*pi units) = 8*pi cubic units.
(Notice that no option coincides with this, there may be a mistake in the options)