Question

Suppose Lauren is working two jobs to help pay for college. One job pays more per hour than the other. Since her boss at the higher-paying job wouldn't give her as many hours as she wanted, she picked up the second job to generate more income. With her course load, 20 hours a week of work is all she can manage, but she wants to make as much money as possible in those 20 hours. Her goal is to get twice as many hours a week at the higher-paying job than at the lower-paying one. How many hours should she work at each job

Answer 1

She will work 6.67 hours at the low paying job and 13.33 hours at the high paying job

Explanation:

Given

`x = Low\ pay\ job`

`y = high\ pay\ job`

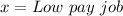
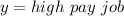
From the question, we have that:

She can only work for 20 hours.

This implies that:

`x + y= 20`

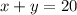
To work 2ce as many hours at the high paying job than the low paying job; implies that:

`y = 2x`

So, we have:

`x + y= 20`

`y = 2x`

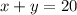
Required

Number of hours at each job

Substitute
`y = 2x` in
`x + y= 20`

`x + 2x = 20`

`3x =20`

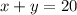
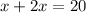
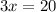
Solve for x

`x = (20)/(3)`

`x = 6.67`

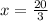
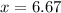
Substitute
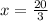`x = (20)/(3)` in
`y = 2x`

`y = 2 * (20)/(3)`

`y = (40)/(3)`

`y = 13.33`

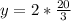
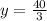
She will work 6.67 hours at the low paying job and 13.33 hours at the high paying job