Answer:
The length of side x in a 30-60-90 triangle is 2√3.
Explanation:
The numbers 30-60-90 are angles, so we need to find the side x of a right triangle with the following information:
θ: is one angle of the right triangle = 30°
α: is the other angle of the right triangle = 60°
a: is one side of the right triangle = √3
b: is the other side of the right triangle =?
x: is the hypotenuse of the right triangle =?
The length of the hypotenuse can be found by Pitagoras:
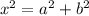 (1)
(1)
So, we need to find the side "b". We can calculate it with the given angles.
From the side "a" we have:

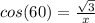 (2)
(2)
From the side "b":
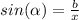
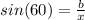 (3)
(3)
Now, we can calculate "b" by dividing equation (3) by equation (2).
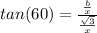
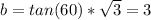
Finally, we can find the length of the hypotenuse with equation (1):
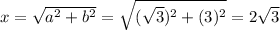
Therefore, the length of side x in a 30-60-90 triangle is 2√3.
I hope it helps you!