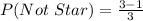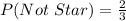Question

It is Marcie's first turn to roll. Which ratio shows the theoretical probability that she will not land on a star space? 1/6 1/3 1/2 2/3

Answer 1

Look at the photo below

Explanation:

Answer 2

`P(Not\ Star) =(2)/(3)`

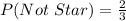
Explanation:

Given

See attachment

Required

Theoretical probability that a roll will not land on a star

From the attachment, we have:

`n = 12` --- Total space

`Star = 4`

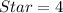
So, the theoretical probability that a roll will land on a star is:

`P(Star) = (n(Star))/(n)`

`P(Star) = (4)/(12)`

`P(Star) = (1)/(3)`

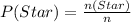
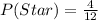
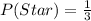
Using the complement rule, the probability that it will not land on a star is:

`P(Not\ Star) = 1 - P(Star)`

`P(Not\ Star) = 1 - (1)/(3)`

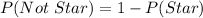
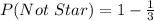
Take LCM

`P(Not\ Star) =(3-1)/(3)`

`P(Not\ Star) =(2)/(3)`