Question

A rigid body of moment of inertia 0.5 kg.M^2 rotates with 2 RPM. How much torque is needed to increase the rotation to 10 RPM in 5 seconds.

Answer 1

T = 0.084 Nm

Step-by-step explanation:

First, we will calculate the angular acceleration:

`\alpha = (\omega_f - \omega_i)/(t)`

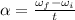
where,

α = angular acceleration = ?

ωf = final angular speed = (10 RPM)(2π rad/1 rev)(1 min/60 s) = 1.05 rad/s

ωi = initial angular speed = (2 RPM)(2π rad/1 rev)(1 min/60 s) = 0.21 rad/s

t = time = 5 s

Therefore,

`\alpha = (1.05\rad/s - 0.21\ rad/s)/(5\ s)\\\\\alpha = 0.168\ rad/s^2`

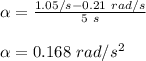
Now, for the torque:

`T = I\alpha`

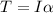
where,

T = torque = ?

I = moment of inertia = 0.5 kg.m²

Therefore,

`T = (0.5\ kg.m^2)(0.168\ rad/s^2)\\`

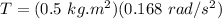
T = 0.084 Nm