Answer:
T = 0.084 Nm
Step-by-step explanation:
First, we will calculate the angular acceleration:
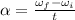
where,
α = angular acceleration = ?
ωf = final angular speed = (10 RPM)(2π rad/1 rev)(1 min/60 s) = 1.05 rad/s
ωi = initial angular speed = (2 RPM)(2π rad/1 rev)(1 min/60 s) = 0.21 rad/s
t = time = 5 s
Therefore,
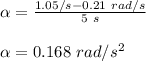
Now, for the torque:
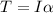
where,
T = torque = ?
I = moment of inertia = 0.5 kg.m²
Therefore,
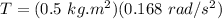
T = 0.084 Nm