Given:
The line passes through the points (2,0) and (4,3).
To find:
The point-slope form of the given line.
Solution:
The point slop form of a line is:
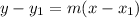
Where, m is the slope and
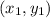 is the point.
is the point.
The line passes through the points (2,0) and (4,3). So, the slope of the line is:
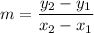
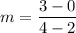
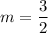
The slope of the line is
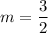 and the point is (4,3). So, the point slope form of the given graphed line is:
and the point is (4,3). So, the point slope form of the given graphed line is:
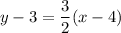
Therefore, the point slope form of the given line is
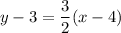 .
.