Answer:
Both volumes are the same
Explanation:
Volume of cylinder =
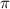
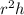
r = radius
h = height
Since area of the circle is given on top,
Area of a circle =
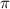
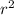
We know the area is 12
12 =
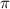
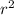 (we need to find r)
(we need to find r)
r =
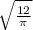
r = 1.954
Now we can find the cylinder's volume:
Volume of cylinder =
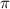
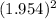 (6)
(6)
Volume of cylinder = 72
To find the volume of the cuboid, we use
Volume of cuboid = lwh
l = length
w = width
h = height
Volume of cuboid = 6 x 4 x 3
Volume of cuboid = 72
This proves that both the volumes are the same.