The analysis above, it seems that the correct answer is C) x=0,1, as both
x=0 and x=1 satisfy the equation. Therefore ,C) x=0,1 is correct.
To find the values of x for which the two functions are equal, set their expressions equal to each other and solve for x:
y=
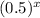 − 1
− 1
Let
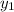 be the value of the exponential function and
be the value of the exponential function and
 be the value from the other function.
be the value from the other function.
So:
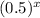 − 1 =
− 1 =

Now, examine the given choices:
A) x=0: Plug in x=0 into the equation to see if both sides are equal:
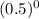 − 1 = 1 − 1 =0
− 1 = 1 − 1 =0
This is not equal to any of the values for
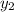
B) x=−1,0: Plug in x=−1 and x=0 into the equation:
For x=−1:
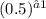 =2− 1 = 1
=2− 1 = 1
For x=0:
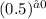 =1 − 1 = 0
=1 − 1 = 0
So, x=0 is a solution.
C) x=0,1: Plug in x=0 and x=1 into the equation
For
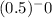 −1=1−1=0
−1=1−1=0
For x=
 −1=0.5−1=−0.5
−1=0.5−1=−0.5
So, x=0 is a solution.
D) The functions are never equal.
From the analysis above, it seems that the correct answer is C) x=0,1, as both x=0 and x=1 satisfy the equation .
Question
An exponential function has the equation y=(0.5)^x-1. Four points from a different function are shown in the table. For what values of x will the two functions be equal? -
A) x=0
B) x=-1,0
C) x=0,1
D) The functions are never equal.